⬅ Exam 2 Study Guide

Please read this page about taking my exams!

Exam format

• When/where
  • During class, here, like normal
  • ~75 minutes
  • it is not going to be “too long to finish”
  • no calculator
• Closed-note
  • You may not have any notes, cheat sheets etc. to take the exam
    • The open-note thing was just for when we were remote
• Length
  • 3 sheets of paper, double-sided
  • there are A Number of Questions and I cannot tell you how many because it is not a useful thing to tell you because they are all different kinds and sizes.
    • But I will say that I tend to give many, small questions instead of a few huge ones.
• Topic point distribution
  • More credit for earlier topics, less credit for more recent ones
  • More credit for things I expect you to know because of your experience (labs, exercises)
• Kinds of questions
  • Some multiple choice and “pick n“
  • Some fill in the blanks
    • mostly for vocabulary
    • or things that I want you to be able to recognize, even if you don’t know the details
  • Several short answer questions
    • again, read that page above about answering short answer questions!!
  • MIPS coding questions which may include
    • tracing (reading code and saying what it does)
    • debugging (spot the mistake)
    • identifying loads and stores in HLL code
    • interpreting asm as HLL code (identifying common asm patterns)
    • fill in the blanks (e.g. picking right registers, right branch instructions)
    • writing some simple asm code (yes!)

Topics

• Languages; Machine and Assembly language
  • Humans understand words, language, abstract concepts; computers understand binary
  • High-level languages (HLLs) focus on “what you want to do” instead of “how to do it.”
  • Low-level languages focus on “how to do it” instead of “what you want to do.”
  • High-level languages are more declarative: you say what you want the result to be, and the computer system “figures out” how to satisfy your request.
  • Low-level languages are more imperative: you say exactly what sequence of steps to do, and the computer executes your steps faithfully.
  • In order for humans to “communicate” with computers, we’ve built many layers of abstraction on top of binary.
    • Human language is the highest-level (most abstract).
    • Natural language e.g. ChatGPT, Siri, Alexa is fairly abstract, but still doesn’t “understand” language the way humans do. Still, they can take an abstract English-like command and turn it into a sequence of steps (or an entire program (which maybe you did for your MIPS assignments (shame on you)))
    • Computer languages like HTML, CSS, and SQL are very declarative - you can’t write a sorting algorithm in HTML - but they have syntax and structure and keywords and stuff. The browser or database engine takes your code and “figures out” how to do what you want.
    • High-level programming languages like Python, JavaScript, Ruby are traditional programming languages with lots of features built into the language/standard library. They let you do a lot with very little code - “semantically dense”
    • Mid-level programming languages like Java and C++ require you to “spell things out” more explicitly (e.g. saying what types the variables are, writing loops instead of having fancy syntactic sugar), but still give you lots of abstraction power (e.g. generics, classes)
    • Low-level programming languages like C give you the bare minimum: functions, variables, structures, pointers, arrays, plus a minimal standard library. It’s up to you, the programmer, to solve all the problems yourself. C is sometimes called “portable assembly” because of its simplicity.
    • Assembly language is a human-readable, textual representation of machine code, and is the lowest layer of abstraction most human programmers care about. It is very nearly 1:1 with machine code (1 assembly instruction = 1 machine instruction), but gives us the ability to use names for instructions, registers, variables, functions, and other things.
    • Machine code is the binary encoding of instructions that a CPU is actually capable of reading and executing. ALL code that a CPU runs is machine code. Compilers exist to translate HLLs into machine code.
  • An instruction is a single command to a computer. it says what to do (verb) and what to do it to (the objects). By analogy, “pick up that can” is a verb (“pick up”) and an object (“that can”).
  • The instruction set is a fixed set of instructions which a CPU is capable of reading and executing. This is only one element of…
  • An instruction set architecture (ISA) is a programmer’s software interface to the hardware. It is a document which specifies many things, such as:
    • the instruction set, as defined above
    • what registers are available
    • how memory is accessed
    • the calling convention: how functions are written and called
    • and many other things
    • but importantly, the ISA does not specify how to built the hardware!!
      • the point of the ISA is to abstract the hardware away from the programmer
      • this way, a machine/assembly program written for the ISA will work on any implementation of the ISA, regardless of who the manufacturer was, what version of the CPU it is, etc.
      • think of an ISA as being a Java interface: defines methods which the programmers uses, but does not include “code” (hardware) for those methods.
  • Common ISAs today are x86 (x86-64 is the most common version) and ARM
    • These two make up the vast majority of computers; all other ISAs make up a tiny fraction in comparison
    • the class uses MIPS, which was never a hugely popular ISA but it was hugely influential and many other ISAs designed in its wake (such as ARM) take many ideas from it.
    • RISC-V is the modern, direct descendant of MIPS, so you would not have much trouble learning to program RISC-V microcontrollers after this course!
• Computer Organization
  • The basic organization of any computer system is:

  

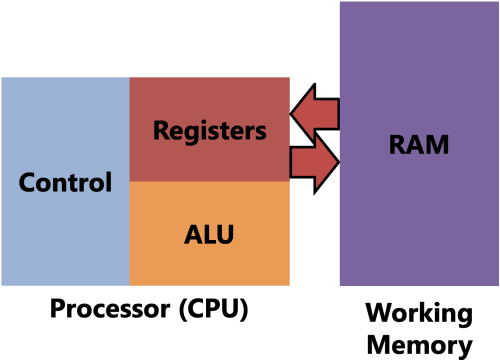
  • the Working Memory or System Memory or “Memory” or RAM (lots of names…) is what holds program instructions, variables, objects, arrays, etc.
  • the CPU or processor is what reads and executes the instructions that make up a program. It is intentionally very limited in what it can do. It can:
    • read numbered lists of instructions (e.g. “step 1, step 2, step 3…”)
    • load numbers out of memory into its registers
    • do simple arithmetic (+-×÷) and logic (AND, OR, NOT, XOR) on those numbers
    • store numbers from its registers back into memory
    • jump to other numbered steps (e.g. “go to step 5”)
    • conditionally decide whether to jump to other numbered steps (e.g. “if x == 10, go to step 7”)
    • this set of operations is Turing complete, as are all programming languages; so programs written in programming languages can be turned into machine code without any loss of capability.
    • the reason this set of operations is so small is because a simpler ISA → simpler hardware → faster and cheaper hardware
  • Neither of these pieces can work without the other. Without the memory, the CPU would have no program to run. Without the CPU, the memory would sit there and do nothing. The CPU computes; the memory remembers.
    • That means this is basically a big ol finite state machine, right…?
  • (The “Control” and “ALU” are not important yet, we’ll learn about those in the last part of the course.)
  • The Registers, on the other hand…
• CPU Registers
  • There are two senses/definitions of “register”:
    • a hardware component which can remember a value, typically multi-bit (this was on exam 1)
    • an element of an ISA: small, fast storage location inside the CPU which the programmer has access to. This is the sense I mean talking about “registers” going forward
  • Registers are small
    • MIPS has 32, 32-bit registers. That’s a total of 128 Bytes of storage. Not very much.
  • Registers are fast
    • Faster to access than the memory. (These days memory is about 100-200x slower than registers, oof. Don’t worry about that until the last part of the course tho.)
  • Registers are inside the CPU
    • Which means the programmer must copy values between registers and variables (loads and stores)
  • Registers are global to the program
    • Your entire program - no matter how many lines of code it is - must use that same set of 32 registers for everything. (This is what the ATV rule and stack are for)
  • For the CPU to perform computations, the values must be in registers
    • The CPU is not “telekinetic” and cannot e.g. “increment a variable in memory”
    • It must instead copy that variable’s value into a register, increment it there, then put the new value back.
  • In MIPS there are 4 main categories of registers:
    • a registers are for arguments to functions. a does not stand for “address”.
    • t registers are for temporary values.
    • v registers are for return values. (and weirdly, selecting which syscall to do)
    • s registers are for saved values (i.e. local variables)
  • There is also the zero register which always holds the value 0 and cannot be changed.
    • 0 is a shockingly useful value that lets the assembler “synthesize” many instructions out of simpler ones using 0 as an operand. e.g. neg t1, t0 does t1 = -t0. But the assembler implements it by turning it into a subtraction from zero sub t1, zero, t0, which does the same thing
  • Registers should not be treated as variables. They are more like hands.
    • In the same way that you accomplish larger tasks by picking up and manipulating many different objects with your same hand(s), the CPU accomplishes larger tasks by picking up and manipulating many different numbers with the same registers.
    • Besides the general categories of meaning explained above, registers do not have a fixed “meaning” or “purpose” the way variables do in HLLs. So it’s totally fine and necessary to reuse the same registers over and over and over again.
• li and move
  • li reg, imm is load immediate
    • load means to put a value into a register
    • immediate means a constant value embedded into an instruction
    • so “load immediate” means “put a constant value into a register”
    • e.g. li t0, 5 puts the constant 5 into t0.
  • move a, b copies between registers: from b into a
    • do not read it as “move a into b”! that’s wrong!!
• Math instructions
  • All math instructions are of the form inst dst, src1, src2 where:
    • dst is the destination (where the result will be placed), and must be a register
    • src1 is a the first source and must be a register
    • src1 is a the second source and can be either a register or an immediate (constant)
  • The instructions are:
    • add dst, src1, src2 (dst = src1 + src2)
    • sub dst, src1, src2 (dst = src1 - src2)
    • mul dst, src1, src2 (dst = src1 * src2)
    • div dst, src1, src2 (dst = src1 / src2)
    • rem dst, src1, src2 (dst = src1 % src2) (“rem” for “remainder”)
  • When doing larger arithmetic calculations, keep in mind the order of operations (PEMDAS)
    • But larger calculations often involve intermediates: results of steps “in the middle” of the expression
    • And in assembly you have to put those intermediates somewhere
    • A good choice for the intermediate is the “final destination” register. e.g. if you want to do some calculation to be returned, you’ll be doing v0 = ..., so v0 is the final destination register, so you can use that for the intermediates.
• Storage
  • There are three places values can be: CPU registers, memory, and persistent storage
    • CPU registers are the fastest but smallest; they are volatile (see below)
    • Memory is much bigger than the registers but also much slower; also volatile
    • Persistent storage is much bigger than the memory but also MUCH slower, but nonvolatile
  • Volatile memory loses its contents when it loses power.
    • So when you power off a computer, the registers and memory get erased.
    • This is why the computer takes some time to start up from powered off: it needs to copy the OS out of the persistent storage into memory.
    • Registers are typically implemented as SRAM: static RAM
      • It’s very fast but requires a lot of silicon area to store 1 bit
    • Memory is typically implemented as DRAM: dynamic RAM
      • It’s slower than SRAM but requires much less silicon to store 1 bit
  • Nonvolatile memory is used for persistent storage: it keeps its contents even without power.
    • e.g. Flash storage is based on Weird Transistors and is used for SSDs, SD cards, USB thumb drives, etc. However it seems to have a finite life and some Flash from the 90s has lost its data!
    • another important technology is magnetic hard disk drives (HDDs) - they have moving parts and can be unreliable because of that, buuuut that magnetically encoded data can be retained for incredibly long times (possibly centuries or millennia).
  • A perfect memory technology would be fast, cheap, dense, and nonvolatile. But there is no perfect memory technology. So, we have to use each of these technologies to their strengths.
• Memory
  • Memory appears to the programmer as a 1-dimensional array of Bytes.
    • everything relating to memory is specified in Bytes, not bits.
  • An address is the number of a location in memory
    • i.e. it’s the “index” into the array of Bytes that is memory. just like an array index, it starts at 0 and increases up to the length of memory minus 1.
  • Each address contains 1 byte, and each byte has an address.
    • This arrangement is called byte-addressable and is the most common arrangement today.
    • A simpler arrangement is word-addressable which is 1 word per address - you’ll be using it on project 2 - but the downside is it’s not as flexible as byte addressing.
• Variables
  • Every variable has 2 parts: address and value
    • Its address is where it is in memory
    • Its value is what it contains (what’s in the bytes at the address)
  • When you declare a variable, the compiler/assembler:
    • Gives it an address
    • Makes the name/label a shorthand for that address
    • Sets aside a certain number of bytes for that variable to “live”
      • No other variables can use those bytes
      • Otherwise they’d overlap and it’d be Bad :(

  • MIPS global variables are declared like so:

      .data # switches to the data segment, where variables live
          x: .word 0
      .text # switches back to the text segment, where code lives
    

    • x is the name, a label - the assembler comes up with an address to use whenever you write x
    • .word says “this variable is a 32-bit integer” - same as a Java int
    • 0 is the initializer (initial value) - without this, the variable won’t exist!
  • You can access variables with the lw and sw instructions:
    • lw reg, var does reg = var
    • sw reg, var does var = reg - the ONLY instruction in ALL of MIPS where the destination is on the right instead of the left.
      • well, the other stores (sh/sb) are the same, but basically “if it’s a store, destination on right; otherwise, destination on left”
  • Setting variables’ values is done with a store (“stores set”)
    • e.g. if you want to do x = 5…

      # x = 5
      li t0, 5
      sw t0, x
    

  • Getting variables’ values is done with a load
    • e.g. if you want to do print_int(x), x needs to go into the a0 register to be passed as an argument, so…

      # print_int(x)
      lw a0, x
      li v0, 1 # print_int syscall number
      syscall
    

  • Read-modify-write operations like x++ can done with a load and a store
    • rewrite in simpler terms: x++ → x = x + 1
    • right side of an assignment happens first; assignment is the last thing done on a line.
    • so x = x + 1 becomes…

      # x++ (or "x = x + 1")
      lw  t0, x
      add t0, t0, 1
      sw  t0, x
    

  • High-level languages hide loads and stores from you, but they’re always there.
    • A variable on the left side of an assignment = is stored into
    • A variable anywhere else on the line is loaded from
    • e.g. in this code:

      int x = f(a, b) + c;
    

    • a, b, c are loaded
    • x is stored
    • (f is a function, not a variable, so it is neither loaded nor stored; it is called)
• Variables bigger than a byte
  • A .word/int variable is 32bits/4Bytes in size. So how is it stored in memory?
  • We logically group bytes together in memory as variables. Note that this isn’t “doing” anything to the memory, and the CPU doesn’t know about this. This is entirely our human abstraction built on top of the “array of bytes.”
  • So for example, a .word which starts at address 0x8000 will be comprised of the bytes at addresses 0x8000, 0x8001, 0x8002, and 0x8003, BUT…
    • The memory address of any value is the address of its first byte.
    • So the address of the above .word is just 0x8000. You don’t need to specify the addresses of the other bytes; they are left implied by the starting address and the size of the value.
    • Prove it to yourself: In MARS, you can assemble a program with variables (e.g. lab 6) and look at the Labels window. Check the “Data” box and you will see the addresses of the variables being a single number like 0x10010000, 0x10010004, 0x10010008 etc.
• Control flow
  • The steps of our program are instructions, and those steps have numbers: the instructions’ addresses
    • But thanks to the assembler, we can refer to those steps by name by using labels
  • There are two categories of code labels:
    • Function labels name entire functions and do not start with an underscore. E.g. main, check_input, char_to_tile
    • Control flow labels are needed because asm has no {} so we need to refer to certain locations within a function. They start with an underscore, e.g. _endif, _loop, _break
  • There are two kinds of control flow instructions:
    • j _label jumps to _label. It always jumps.
    • b__ a, b, _label is a conditional branch: it’s called a “branch” because it goes one of two ways, like a branching path or a tree branch.
      • There are 6 conditions:
        • beq (a == b)
        • bne (a != b)
        • blt (a < b)
        • ble (a <= b)
        • bgt (a > b)
        • bge (a >= b)
      • a must be a register, but b can be either a register or an immediate
        • think by analogy to sub dst, a, b, because comparison is done by using subtraction
  • Conditional branches go to the label if their condition is true (satisfied), but if the condition is not satisfied, they go to the next line
    • e.g. beq t0, 10, _label says “if t0 == 10, then go to _label, else go to the next line”
  • Unfortunately that means that there is a mismatch between the way we write conditions in ifs in Java vs. how they work in asm.
    • In Java if(a == b) { stuff(); }
      • If a == b, stuff() is run (“go to next line”)
      • If a != b, stuff() is skipped (“go somewhere else, to closing brace”)

    • In asm

        beq a, b, _endif # a, b are just placeholders here
        jal stuff
        _endif:
      

      • if a == b, jal stuff is SKIPPED! (“go somewhere else, to _endif”)
      • if a != b, jal stuff is RUN! (“go to next line”)
    • When writing ifs in asm, you have to invert the condition because in asm, the condition is really answering the question “when do we skip the contents of the if”
      • So the above code would be fixed by changing it to bne
  • However, you don’t always invert conditions. E.g. do-while, “simple” for loops
    • These test the condition at the end of the loop, so we do want to go backwards when the condition is true
• Arrays
  • An array is a collection of variables where:
    • All the variables are the same type
    • All the variables are consecutive in memory
    • Because they are all the same type, they are therefore all the same size
    • And because they’re all consecutive and the same size, they are therefore equidistant from one another. That’s really the key
  • e.g. arr: .word 1, 2, 3 is 3 words/12 bytes of memory; each item of the array is 4 bytes apart because a word is 4 bytes.
    • Note that neither the assembler nor the CPU have any concept of “an array” like we have in Java. An array is “something you do” instead of “an object.” This also means that arrays don’t “know” how long they are, and therefore accessing an array out-of-bounds in asm will lead to confusing behavior!
• Accessing arrays in MIPS
  • The address of A[i] is A + i×S where:
    • A is the address of the array (in asm, the label is the address)
    • i is the index you want to access (in asm, typically a register)
    • S is the size of one item in bytes
      • for .word arrays S=4
      • for .half arrays S=2
      • for .byte arrays S=1
      • etc.
  • Why? Because this is fast.
    • A + i×S can be computed in constant time (O(1)) no matter what i is.
    • This is in contrast to e.g. a linked list, where accessing an item is linear (O(n))
    • Arrays are the fastest data structure available to you. (Caching also helps make them fast, but that’s a CS1541 topic)
  • To access an array, you must first multiply the index by the size, then use that multiplied index inside the parentheses of this form of load/store:

    # a0 = arr[s0], where arr is an array of .word
    mul t0, s0, 4   # t1 = s0 * 4
    lw  a0, arr(t0) # a0 = arr[s0]
  

  • Recall that the silly arr(t1) syntax means arr + t1 - that is, “start at the address of arr, then move over by t1 bytes in memory”
  • For .byte arrays, there is no need for a mul because S=1
• Alignment
  • For any n, the address of an n-byte value must be a multiple of n.
    • e.g. words are 4 bytes. so, their addresses must be multiples of 4 (0x00, 0x04, 0x08, 0x0C, 0x10, 0x14, 0x18, 0x1C,...)
    • BUT THAT WAS JUST AN EXAMPLE. words are 4 bytes, but not everything is.
    • e.g. doubles are 8 bytes, so their addresses must be multiples of 8 (0x00, 0x08, 0x10, 0x18,...)
  • Failing to respect alignment on MIPS causes your program to crash.
    • e.g. if you try to load a word from an address that ends in hex 3, it will crash.
    • On other architectures, it may crash, or it may work but be a lot slower than an aligned access.
  • Why does the CPU care?
    • This is a leaky abstraction. Physically, most memory is implemented as a 2D array of bits, where only one row can be accessed at a time, and that is a physical limitation.
    • Unaligned memory accesses might require accessing 2 or more rows simultaneously, which is physically impossible. So, MIPS just forbids it. It’s easy enough to write code that respects it.
• Functions (Theory)
  • a function is a named piece of code with inputs and outputs
    • the name should say what the function does - functions are verbs, actions
    • inputs are arguments
    • outputs are return values and/or side effects (see below)
    • the code of a function is arguably the least important part - the whole point of a function is to abstract away the code, so that the caller doesn’t have to know how it works
      • e.g. you don’t know how println works. but you call it. and it does its job.
  • side effects are “anything the function affects outside of itself” and includes a wide variety of behaviors
    • input and output are a very important kind of side effect
    • other examples include modifying global variables and modifying objects/arrays that were passed in
    • side effects are useful but hard to reason about because they make it possible for a function to do different things depending on how many times it’s been called
      • functions without side effects are like the ones from math, and are easier to comprehend
  • Why are functions useful?
    • They let us name steps of our programs, so that other code becomes more readable
    • They let us avoid copypasting code by making that code reusable - just call it again!
    • They let us split up bigger problems into smaller ones
    • We can take the outputs of one function and pass them as inputs to another
      • This lets us break complex multi-step problems into smaller pieces, like I already said
    • And in more advanced contexts, we can pass functions as arguments to other functions, in order to parameterize actions
      • (You don’t need to know this but a really common and useful application of this is sorting: by passing a comparison function to a sort function, we can define how items are compared, so that the same algorithm can sort ascending, or descending, or by multiple pieces of data, or whatever.)
  • Function vocab
    • The verb call means “to run a function” and it looks like f() in most languages.
      • This is the only valid definition of “call.” You cannot call a variable. You cannot call a class. You cannot call a file. You cannot call a return value. You cannot call anything that is not a function.
    • The caller is the function which performs a call, and the callee is the function being called.
      • So if main calls println, main is the caller and println is the callee.
    • The verb return is a little tricky because there are two parts to returning:
      • returning a value from the callee to the caller
      • returning control from the callee to the caller (that is, resuming execution in the caller)
  • The call mechanism
    • A call consists of:
      • Remembering our place in the caller (i.e. “where to come back to” when the call is done). This is the return address.
      • Jumping to the callee so it starts to execute.
    • A return consists of:
      • (Optionally) putting the return value where the caller will be looking for it.
      • Jumping back to the return address so that the caller resumes.
    • This process can be repeated arbitrarily deep
      • If main calls func1 which calls func2 which calls func3…
      • then when func3 is done func2 resumes
      • then when func2 is done func1 resumes
      • and finally when func1 is done main resumes
• Functions (in MIPS)
  • The program counter (PC) register holds the address of the current instruction
    • (it’s the “yellow line” instruction in MARS)
    • After non-control-flow instructions, it’s incremented by 4: pc = pc + 4
      • All MIPS instructions are 4 bytes long, so “the next instruction” is always at “the current address plus 4”
      • So pc + 4 is “the address of the next instruction.”
    • Jumps replace the PC with their address
      • j _label does pc = address of _label (some number)
    • Branches either do the same as a jump, or they do the same as a non-control-flow instruction (go to the next instruction at pc + 4)
  • The call instruction in MIPS is jal func
    • jal = “jump and link”, though the “and link” step happens “first”
    • jal func does:
      1. ra = pc + 4 - set the return address register ra to the address of the instruction after the jal
      2. pc = address of func just like a j
  • The return instruction in MIPS is jr ra
    • It does pc = ra, very simple
    • But it only returns because jal set up ra for it to use
  • Think of ra like a bookmark:
    • it marks our place in the caller where we need to go back to once the callee is done
    • jal is the only instruction which puts the bookmark in place. j and branches do not set ra and cannot be used in place of it.
      • if you try to j or branch to a function, then the jr ra at the end of it will malfunction! it will either try to jump to address 0 and crash, or it will use an old, smelly, outdated ra which doesn’t point back to the jump/branch and will take us somewhere unexpected.
  • With a single return address ra, we can only go one function call deep.
    • Let’s say main calls func1 which calls func2. What will happen is…
      • the jal func1 in main sets up ra to point into main.
      • the jal func2 in func1 sets up ra to point into func1, overwriting the return address to main!
      • then func2 runs normally and returns normally…
      • but when func1 tries to return, it will instead jump back into the middle of itself, right after jal func2, causing it to be trapped in an infinite loop, unable to return to main.
    • By analogy to bookmarks, it’s like trying to use one bookmark (ra) to mark your spot in 2 books at the same time. It’s impossible. When you move the bookmark from one book, you lose your place in it.
• Calling Convention
  • Honor system used to let multiple functions work together
    • Remember that all functions share the registers so this is important!
  • Makes them agree on:
    • How arguments are passed from caller to callee
    • How values are returned from callee to caller
    • How control flows from caller to callee, and then back again
    • What goes on the stack
    • Who is allowed to use which registers, and for what purposes
    • Which registers must be preserved across calls, and which can be trashed
  • MIPS calling convention arguments and return values:
    • caller places arguments in a registers starting with a0 before the jal
    • callee is written to assume the caller has done this
    • callee places return value in v registers starting with v0 before returning
    • caller is written to assume the callee has done this
    • Neither the assembler nor the CPU know about this, ensure you are using it correctly, will catch you when you mess up, etc. it is all just an honor system. As long as all code follows this rule, it will work.
• The call stack (“the stack”)
  • A region of memory that is set up for you by the OS (or MARS) before main runs
  • Used to hold information about function calls that cannot fit into the registers alone
    • Remember, registers are tiny, and sometimes multiple functions need to use the same registers for different purposes (like different bookmarks in ra, or different arguments to functions)
  • You can think of the stack as a dynamically-sized array
    • Pushing puts a value on top of the stack (“appends it” to the array)
    • Popping removes a value from the top of the stack (“removes” the last item of the array)
  • Access stack through the special stack pointer register sp
    • You can load and store from the stack with e.g. lw t0, (sp) - “load a word from the address held in sp into register t0”
    • You can also specify offsets with e.g. lw t0, 4(sp) to load from sp + 4
      • Commonly used when accessing “stack-based local variables,” which are common in HLLs but not so much in hand-written asm
  • To push:
    1. sub sp, sp, 4 (to make space for the new value)
    2. sw reg, (sp) (to store register reg in that new space)
  • To pop:
    1. lw reg, (sp) (to get the value back off the stack into reg)
    2. add sp, sp, 4 (to move the pointer back up to where it was before the push)
  • We also have the push reg and pop reg pseudoinstrutions to shorten these
  • To solve the “only one function call deep” problem:
    • push ra at the beginning of every function (except main)
    • pop ra at the end of every function (except main) right before the jr ra
• Activation Records and recursion
  • A stack is a perfect match for the way function calls work:
    • Whenever a function is called, it pushes an activation record (AR)
      • An AR contains saved registers (like ra!), and in HLLs, local variables
      • AR != ra - a saved ra (return address) is pushed as part of an AR (activation record)
    • Whenever a function is about to return, it pops the AR
    • This order of creating and removing ARs perfectly matches the way that functions begin and end - functions end in the opposite order of when they’re called, and that’s how values come off of stacks
  • The stack is also necessary to make recursive functions work:
    • Every time a recursive function calls itself, a new copy of its local variables is pushed
    • So there can be multiple activation records for the same function on the stack at the same time, each with different values for the local variables
      • There is an example of this on the Materials page
• ATV Rule
  • Any function is allowed to change the a/t/v registers at any time for any reason! :))))))
    • this makes the a/t/v registers easy to use: you never need to check if “another function is using them.” you just go ahead and use them. use t0 in every function, it’s totally fine.
      • it also means you never need to push/pop a/t/v registers
  • but there is a negative consequence: a caller cannot assume that the a/t/v registers have the same values after a jal as they did before it.
    • basically, a/t/v registers are not “safe”
    • when you jal func, you are handing all the registers over to func and it is totally allowed to use a/t/v regs as scratch paper
  • so on the line after the jal, think of the a/t/v registers as containing “old leftover food” - they may be safe, they may not! don’t risk it!
    • e.g. if you do li t0, 5, then jal, you cannot expect t0 to still be 5 after the jal.
    • if you want known values in them after a jal, you have to put values back into them.
  • remember: registers are not variables.
    • do not initialize all the registers at the top of a piece of code and use them throughout.
    • put values into the registers immediately before you use those values, and you will avoid so many headaches.
• S register contract
  • Instead of using the clunky “stack locals”, we can use s registers in place of local variables.
  • The contract is: when a function returns, the s regs must be “put back to the way they were” when it was first called.
    • That is, when you get to jr ra, the s regs must have the same values as they had right after the function label.
  • A function that never changes the s regs satisfies this contract by default, because their values never change.
  • But if you want to use some s register sx, you must:
    • push sx at the beginning of the function that wants to use it
    • pop sx at the end of the function that wants to use it
  • By following this protocol, it’s as if every function gets its own s registers
    • But everyone has to follow the protocol, or the guarantee is gone!
  • We don’t really need to use s regs very often.
    • If you find yourself using 3, 4, 5, 6 etc. on each function, you’re overusing them.
    • They’re like salt - best used in moderation
    • Most of the time, you only need t regs, sometimes a or v when doing function calls/returns
    • s regs are often useful as for loop counter variables - because many for loops have jals inside them, which makes s regs the only option that doesn’t violate the ATV rule.
• Non-word-sized loads and stores
  • Besides .word (equivalent to Java int) and lw/sw, we have…
    • Java byte is MIPS .byte and we use lb/lbu and sb to access
    • Java short is MIPS .half and we use lh/lhu and sh to access
  • But what’s up with lb/lbu and lh/lhu?
    • Registers are 32b. .byte are 8b. .half are 16b.
    • So when you load a byte or a half, you need to come up with extra bits to fill in the rest of the register.
  • going from a smaller number of bits to a larger number, while preserving the value is called extension and there are two “flavors”:
    • lbu and lhu perform zero extension: write 0s in front of the number.
      • the u is for unsigned, that’s why.
      • so a byte 0x10 (16) will be zero-extended to 0x00000010 (still 16)
      • and a byte 0xA0 (160) will be zero-extended to 0x000000A0 (still 160)
    • lb and lh perform sign-extension: write copies of the sign bit in front of the number in binary.
      • you have to think about the binary representation for it to make sense.
      • a byte 0x10 (+16) has binary representation 0001 0000.
        • The MSB is 0, so put 0s in front in binary: 0000 0000 0000 0000 0000 0000 0001 0000
        • this looks like 0x00000010 hex.
      • but a byte 0xA0 (-96) has binary representation 1010 0000:
        • The MSB is 1, so put 1s in front in binary: 1111 1111 1111 1111 1111 1111 1010 0000
        • or 0xFFFFFFA0 hex! The 1s in binary become Fs in hex.
  • going from a larger number of bits to a smaller number is called truncation.
    • there is only one “flavor”: cut bits off the left side. that’s why there’s only sh and sb.
      • (Don’t confuse this with floating-point truncation, if you’ve heard of that - that cuts off the fractional places and gives you an int)
    • but this is a lossy operation: you are throwing away bits, and if the bits you throw away are contributing to the value, the truncated value will differ from the original!
    • it’s your responsibility as the programmer to make sure that the value being stored is in the valid range for the target number of bits.
• All data transfer instructions
  • If we put all the data transfer instructions together in one diagram:

  

• Endianness
  • it is a rule which is used to decide the order of BYTES
    • when going from things bigger than a byte to bytes
    • or vice versa.
  • it comes up in…
    • memory (cause it’s an array of bytes)
    • files (also arrays of bytes)
    • networking
  • big endian stores the big end (most significant byte) first.
    • “read it in order”
    • 0xDEADBEEF is stored in memory in the order 0xDE, 0xAD, 0xBE, 0xEF in ascending addresses
      • 0xDE is at the first address
    • feels “natural” because we write numbers big-endian, but it’s not necessarily “better” than little-endian
  • little endian does the opposite, stores the least significant byte first.
    • “swap the order”
    • 0xDEADBEEF is stored in memory as 0xEF, 0xBE, 0xAD, 0xDE in ascending addresses
      • 0xEF is at the first address
    • Notice that we don’t swap the hex digits or the bits, we swap the order of entire bytes
  • but 1-byte values and arrays of 1-byte values are not affected by endianness
    • because they aren’t chopped up when loading or storing
• Fractional numbers
  • Fractional places are negative powers of the base
  • In binary that means they are the 1/2, 1/4, 1/8, etc.
    • converting fractional binary numbers to base 10 still works the same way it always has: add up place values for 1 bits
    • e.g. 1.101 binary is 1 + 1/2 + 1/8 = 1 5/8
  • Only fractions whose denominators are composed of prime factors of the base will terminate when expressed in fractional places.
    • In base 10 that means any denominator of the form \(2^x5^y\)
      • so 1/2, 1/5, 1/10, 1/20, 1/25, 1/50 etc. terminate
      • but 1/3, 1/7, 1/9 do not
    • In base 2 that means only denominators which are powers of 2…
      • so 1/2, 1/4, 1/8 etc. terminate
      • but even something like 1/10 (base 10) does not terminate in binary!
  • nonterminating ≠ irrational
    • nonterminating - infinitely long, but repeats (e.g. 1/3. it is rational! it’s a ratio!)
    • irrational - infinitely long, but never repeats (e.g. π)
  • We work with “infinitely long” fractions in math all the time…
    • but if we are forced to stop after a certain number of places, the number we get is only an approximation of the real value.
    • e.g. 1/3 ≠ 0.3333333. It’s only an approximation of the real value of “0.3 repeating”
• Floats (which includes both float and double)
  • Floats are represented as fixed-length binary fractional numbers.
    • This means common fractions like 1/10 and 1/100 - which come up constantly in MONEY - are NOT EXACTLY REPRESENTABLE IN FLOATS
    • You should NEVER use floats for money.
    • Money uses base-10 fractions, so the only way to calculate it correctly is in base 10.
      • e.g. Java has BigDecimal for this purpose
  • Float arithmetic is also not associative
    • that is, (a + b) + c may not equal a + (b + c)
    • that’s because there is a “rounding” step performed after every operation
    • so it’s more like round(round(a + b) + c) vs. round(a + round(b + c))
  • Floats aren’t useless/scary/bad though. Some numbers can be represented exactly.
    • integers (for some range) are exact.
    • any fraction with a power-of-2 denominator (for some range) are exact.
• IEEE-754
  • the one and only standard for floats that all CPUs and software now use
    • it is to floats as 2’s complement is to signed ints
  • defines 2 formats
    • single precision (float): 1 bit sign, 8 bit exponent, 23 bit fraction (32b total)
    • double precision (double): 1 bit sign, 11 bit exponent, 52 bit fraction (64b total)
    • (it actually defines more than 2 formats but these are the widespread ones)
  • unlike ints, floats use SIGN-MAGNITUDE
    • negating is simple - flip the sign bit and only the sign bit
    • downsides: two zeroes (+0.0 and -0.0), arithmetic is more complicated (not getting into it)
  • if you have a number in base-2 scientific notation, you can encode it like so:
    • sign field is 0 for positive, 1 for negative (just like ints)
    • fraction field is the bits after the binary point, left-aligned, with trailing 0s to fill it
      • because the bit before the binary point is always 1, we don’t bother storing it in the variable!
      • that extra 1 is “reconstituted” in the internal CPU circuitry when the value is loaded, however.
      • this gives us effectively a 24-bit significand, instead of 23 bits.
    • exponent field is an unsigned number, calculated as original exponent + bias
      • e.g. for single-precision, bias is 127. so an exponent of +7 is encoded as unsigned 134, and an exponent of -100 is encoded as unsigned 27.
      • it’s bizarre. it’s called “excess-k” encoding, and they chose this for sorting reasons? I don’t fully understand it myself
      • on the exam, you will be given the bias constant for whatever format it is.
  • if you have an IEEE-754 float, you can turn it into a number in base-2 scientific notation like so:
    • sign field is 0 for positive, 1 for negative (just like ints)
    • write 1. then put the bits of the fraction field after it (ignore trailing 0s)
    • decode exponent field as an unsigned int, then subtract bias
      • e.g. for single precision, an encoded exponent field of 0111 1110 is unsigned 126;
      • then 126 - 127 = -1 as the decoded exponent
    • then it’s × 2 to the decoded exponent.